I would like to preface this by saying I am not a computer scientist, I am not a researcher, I am just someone who is interested in exploring technical topics for fun.
If you are looking for precise mathematical descriptions of how to create a programming language, this post probably isn't for you. If you are someone who is interested in tinkering with creating parsers/interpreters for programming languages, and wants to know the process I went through, then this is definitely for you!
Goals
So just why would I want to create a programming language?
For fun!
I created a basic interpreter at University, which had the ability to read streams of numbers from stdin, apply mathematical operators against the input stream (+-*/ etc.), and then output the result to stdout. This was a project I deeply enjoyed, and have been meaning to do something a bit more in depth for almost 10 years now.
I want to create something that supports most basic data types such as strings, booleans and numbers. I want it to support some complex data types like lists and records (JSON too), and I also want it to have a small library of data structures/utilities included by default.
Then there are all the standard features required to make a language turing complete, such as looping and functions. Technically you only need recursion to have a turing complete language, for example TypeScript's type system is actually turing complete, but including common looping constructs is not too difficult.
The aim for this project is mainly to support computation/data manipulation in a nice way, so no complex IO/network related support. I won't expend much effort on generating nice error messages to start with, though I won't rule this out later if I feel like it.
Avoiding third party tools
The interpreter I created at University made use of tools like lex and yacc. It was written in OCaml, and used lex and yacc for OCaml.
lex and yacc are tools which generate a parser for you, using bottom-up parsing. They take your description of a language, a context free grammar, and convert this into a program which can parse a program written in the language you specified with your grammar, a "compiler compiler".
I wanted to have a go at creating a language parser with zero dependencies. This might be a bit masochistic, but would force me to explore topics in more depth than I ever have before. Since yacc uses bottom up parsing, it is a bit more powerful than a standard recursive descent parser, the type of parser I will be using. yacc can handle languages that are left recursive. Recursive descent parsers cannot handle left recursive grammars, so I will be forced to use right recursion instead.
lex and yacc allow you to specify precedence. This feature allows you to specify a grammar that branches over a set of rules, whilst retaining predictability of the parser. This is something else I will lose out on by manually implementing a recursive descent parser. However, it is possible to define precedence through your language's grammar itself, which is what I intend to use instead - another topic I haven't explored much before.
Please take a look at the table of contents for specific areas you might be interested in, I will take a pragmatic look at operator precedence and operator associativity in later sections.
Compiling back to JavaScript
I want to have a go at transpiling my toy language back to JavaScript, making it possible to run a program as "native" code in the browser. The interpreter I plan to create for my language could run in the browser of course, but will be much slower than running JavaScript.
This is another feature that won't have all that much practical use, other than satisfying my curiosity.
I will likely try to package this as a webpack plugin, identifying usage of the language in a codebase, and applying the JavaScript transpilation on the identified code.
Focus on immutable data
The last goal I will focus on for the language, is making complex data structures immutable. It will include operators to manipulate data structures, returning new copies of data, rather than references to existing data. Reassignment of variables will be allowed, but mutating data structures will be impossible.
For instance, in JavaScript, you can mutate data structures like so:
const myJsonValue = {
a: 1,
b: 2,
};
const newJsonValue = myJsonValue;
// Mutates the original record
newJsonValue.a = 2;
myJsonValue.a; // 2
I hope to be able to implement this using immutable operators instead, that clone the data, and return new values instead of assigning to the existing values.
// In my toy language
let myJsonValue = {
a: 1,
b: 2,
};
// Copies myJsonValue at this point as a new record
let newJsonValue = myJsonValue;
newJsonValue == myJsonValue; // false
// <- is an operator that merges { a: 1 } into newJsonValue
let finalJsonValue = newJsonValue <- { a: 1 };
finalJsonValue == newJsonValue; // false
finalJsonValue == myJsonValue; // false
One loose goal this will accomplish, is that this language would complement modern frontend frameworks and tools such as react and redux, of which immutable data is a core component of how they work with respect to state.
I still need to investigate how this will affect things like circular references in records, but it may mean that this language only support non-cyclical records.
By this I mean in JavaScript you are allowed to have circular references:
const myRecord = {
some: 'value',
};
// Perfectly legal in JavaScript
myRecord.itself = myRecord;
// In my toy language
myRecord.itself = myRecord; // error
Anything you can't call JSON.stringify on in JavaScript, might end up not being legal in my toy language.
So what's involved in building a programming language?
There are three main steps in having a working programming language that I will be covering. Lexical analysis, parsing, and interpretation/transpilation.
There are of course other avenues such as code compilation, where code from an abstract syntax tree is converted to lower level code such as machine code, possibly performing code optimisations on top of this, but I won't be covering this topic.
Lexical analysis
This part is actually very simple. It is essentially looping through the input source code character by character, and seeing if the characters match one of the lexical analysis rules you specify.
Some pseudo-code for this process might look like:
// Matcher rules
const numberLiteral = /\d+/;
const additionOperator = /\+/;
const subtractionOperator = /-/;
const consumeUsingMatcher = (source, regex) => {
// Function that removes the matched content
// from the given source code
};
// Main loop for generating a list of tokens
const lex = (sourceCode) => {
const tokens = [];
while (sourceCode.length > 0) {
if (numberLiteral.test(sourceCode)) {
tokens.push({ type: 'NUMBER_LITERAL', content: /* extract value from characters */ });
sourceCode = consumeUsingMatcher(source, numberLiteral);
} else if (additionOperator.test(sourceCode)) {
tokens.push({ type: 'ADDITION_OPERATOR' });
sourceCode = consumeUsingMatcher(source, additionOperator);
} else if (subtractionOperator.test(sourceCode)) {
tokens.push({ type: 'SUBTRACTION_OPERATOR' });
sourceCode = consumeUsingMatcher(source, subtractionOperator);
} else {
throw new Error('Unrecognised token');
}
}
return tokens;
};
The key here is to not try to apply any semantic meaning to the character you see inside the source code.
E.g. you wouldn't try to recognise an expression like 1 + 2 as an ADDITION_OPERATION, because
addition can apply to other tokens other than number literals too, such as a + 2, (a - b) + 2 and so on.
You would instead recognise it as three separate tokens, a number literal 1, an addition operator
+ and another number literal 2.
Given a source string like so:
let a = 1 + 2 + 3;
You would hope to produce a list of tokens that looks something like this:
[
{ type: 'VARIABLE_DECLARATION' },
{ type: 'IDENTIFIER', value: 'a' },
{ type: 'ASSIGNMENT' },
{ type: 'NUMBER_LITERAL', value: '1' },
{ type: 'ADDITION_OPERATOR' },
{ type: 'NUMBER_LITERAL', value: '2' },
{ type: 'ADDITION_OPERATOR' },
{ type: 'NUMBER_LITERAL', value: '3' },
{ type: 'SEMI_COLON' }
]
As you can see, the tokens with variable contents will have content associated with them, whereas the tokens which do not ever change (addition operator, semi-colon etc.) don't need the source string anymore. It doesn't matter if you do retain the source string for these tokens, but it won't be needed in any subsequent steps.
No parsing of the content is done at this stage either. Eventually we will want to convert the strings '1', '2', '3' into real numbers which we can use within the interpreter, but this can be done during the parsing step.
During lexical analysis, you could also do additional things such as tracking the line and column numbers where the tokens appeared in the source code. This would primarily be used for things like generating helpful error messages.
Parsing
This is the meat of the work in hand crafting a parser and interpreter. This step converts the input stream of tokens into an AST (abstract syntax tree).
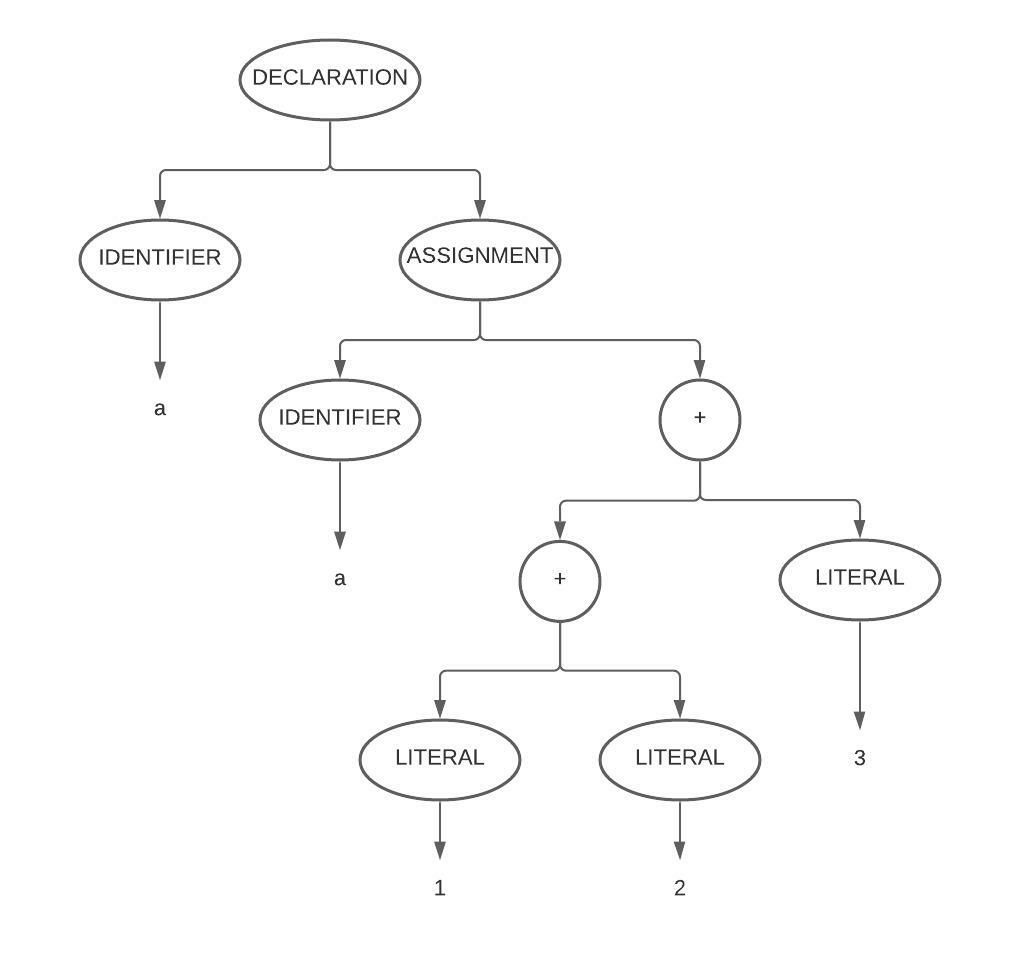
Example AST for `let a = 1 + 2 + 3;`
The image above shows an outline of the kind of thing we will need to achieve.
Take note of the placement of addition operators in the tree, as this affects the order the operators will be applied in. This AST is left associative, see the operator associativity section for more on this.
I will go through in detail how I generate ASTs like this in the parsing section.
Interpretation
This stage takes an abstract syntax tree, and runs the program defined by it. The output we would want for our example expression:
let a = 1 + 2 + 3;
would be that the variable a has a value of 6, and is stored in the root scope of the application.
Obviously this wouldn't be a very useful program, but it is still a program nonetheless incorporating a couple of
interesting features - storing variables and mathematical operators.
I will go through the exact details of my interpreter in a later post.
Creating a lexer
The real implementation for this is very similar to the pseudocode I showed in the lexical analysis section.
I defined a factory function, which creates a function to match against an input string, which returns an object with some methods and properties relating to if a source-code-string was matched against the given regex.
// Takes a regex to match source code, and the string token
// that will be created if it does match
const makeTokenMatcher = (regex, token) => (str) => {
const match = str.match(regex);
return {
// Test that the string was matched (requires
// the regex to have a capture group containing the
// part we are interested in)
matched: Boolean(match?.[1]),
// The token we will create
type: token,
// Method to advance along the source code,
// removing the substring we just matched
consume: () => str.replace(match[0], ''),
// The actual content of the token if it's dynamic,
// e.g. for identifiers and literals. Again this requires
// a capture group to capture the bit we are interested
// in.
content: match?.[1],
};
};
To use this factory function, it's as simple as doing things like this:
// Match any number, capturing the number in
// a capture group
const numberLiteralMatcher =
makeTokenMatcher(/^(\d+(\.\d+)?)/, tokens.NUMBER);
I then create an array of all possible matchers, and loop on the source code until it is fully consumed, or a substring isn't matched:
const tokenMatchers = [
numberLiteralMatcher,
// Other matchers for keywords/operators go here
];
const lex = (sourceCode) => {
const tokens = [];
while (sourceCode.length > 0) {
const matcher = tokenMatchers.reduce((acc, matcher) => {
// If we've seen something already, skip this matcher
if (acc) return acc;
const result = matcher(sourceCode);
// If there was a match, return this matcher
if (result.matched) return result;
// Otherwise continue
return acc;
}, false);
if (!matcher) {
// Error, there was a substring in the source code we
// didn't recognise
throw new Error(`Could not find a token for: "${source}"`);
}
// Extract the parts we'll need for the parser,
// and add to our token list
tokens.push({
type: matcher.type,
content: matcher.content,
});
// Advance along the source code by the bit we just matched
sourceCode = matchingToken.consume();
}
return tokens;
};
That's it, job done for our lexer!
One caveat we need to be mindful of, is that this approach will not work if you have
defined regexes that are ambiguous. By this, I mean if one regex covers another regex, the token
that gets matched will depend purely on the order of your tokenMatchers array, which is not what we want.
Ideally the tokens that get matched would always be the same, regardless of the order of matchers in the
tokenMatchers array.
As an example, you could define an ASSIGNMENT token with a regex:
const assignmentMatcher =
makeTokenMatcher(/^(=)/, tokens.ASSIGNMENT);
If you subsequently defined a comparator regex, e.g.
const comparisonMatcher =
makeTokenMatcher(/^(==)/, tokens.COMPARISON);
We are now in a situation where depending on the order the matchers get tested against the source code, you
will either end up with two ASSIGNMENT tokens, or a single COMPARISON for the string '=='.
To get around this issue, I used negative lookahead expressions in some of my regular expressions, to ensure the matchers are all unique and unambiguous. So my assignment matcher became:
const assignmentMatcher = makeTokenMatcher(
// Match '=', only if it's not immediately followed
// by another '='
/^(=(?!=))/,
tokens.ASSIGNMENT,
);
Creating a parser
I have already mentioned tools that assist with generating parsers automatically from grammars. Creating a parser that will work without these tools is new to me. Whilst you can hand-code parsers using bottom up parsing, the easiest and most intuitive way is with recursive descent parsing.
As the name suggests, you create functions associated with your grammar, typically one function per non-terminal, and recursively descend down your grammar definitions, until you reach a terminal symbol, or encounter an invalid expression.
If we look at the addition component from our example in the previous section:
1 + 2 + 3;
we could define a grammar which describes this expression.
<addition> ::= <addition> "+" <addition> | <numberLiteral>
<numberLiteral> ::= LEAF
Looking at this grammar, it intuitively makes sense. Addition is allowed, which itself can be an addition expression summed with another number expression, or a number literal. We allow references to additions as the left and right operand for addition, so that we can cover expressions like this, which can be arbitrarily long:
1 + 2 + 3 + 4
A number is the terminal symbol in our grammar, so when we reach this we have finished creating our tree.
An attempt to codify this grammar might look something like the following:
function addition(tokens) {
const additionLeft = addition(tokens);
// Do we have an addition on the left?
if (additionLeft) {
// Don't need to consume the tokens, the recursive
// call to "addition" will handle this for us
// Did we see "+"?
if (tokens[0].type === 'ADDITION_OPERATOR') {
// Consume the token we just matched
tokens.splice(1);
const additionRight = addition(tokens);
// Do we also have an addition on the right?
if (additionRight) {
// We do, so we have an addition operator
return {
type: 'ADDITION_EXPRESSION',
leftOperand: additionLeft,
rightOperand: additionRight,
};
}
}
}
// If we get here, we didn't see an addition.
// The only other possibility from our grammar for
// addition is that it is a number literal
return numberLiteral(tokens);
}
function numberLiteral(tokens) {
if (tokens[0].type === 'NUMBER_LITERAL') {
// Consume the token we just matched
tokens.splice(1);
return {
// type of the AST node, it has the same name as
// the token name in this case, but often it will
// be different
type: 'NUMBER_LITERAL',
// Parse the string value we made available during
// our lexing step
value: parseFloat(tokens[0].content),
};
}
// Not a number literal, no other options for numbers
// so return false
return false;
}
This looks like it matches our grammar, but unfortunately this does not work for recursive descent parsing. If we think
through what will happen when we call addition with our program's tokens, it first checks if the left operand is
an addition. So far we have addition -> addition. OK sure that's fine, so what happens in the body of our next
call to addition? That's right, we check if the left operand is an addition, so now we have addition -> addition -> addition. You can probably see where this is going, we're going to have a stack overflow...
Left recursion vs right recursion
So how can we possibly create a working parser using recursive descent? It turns out the answer is in how we define our grammar in the first place. Recursive descent parsers only work on a subset of possible context free grammars. In other words they are not powerful enough to work on grammars that are left recursive.
Left recursion
Our example in the parsing section section was a left recursive grammar. A bit more formally (not super formal, I am not a computer scientist after all), left recursion is where our grammar allows non-terminal expressions on the left side of our grammar sequences, i.e. exactly what we saw before:
// we have a non-terminal "addition" on the left side
// of the sequence (and on the right side)
<addition> ::= <addition> "+" <addition> | <numberLiteral>
We need to use right recursion instead, a form of context free grammar that recursive descent parsers can handle.
Right recursion
Right recursion is where we allow non-terminal expressions on the right side of our grammar sequences only.
This is a right recursive version of our grammar for addition expressions:
<addition> ::= <numberLiteral> "+" <addition> | <numberLiteral>
<numberLiteral> ::= LEAF
At a first glance, it might not look like this grammar can handle infinitely long sequences of addition. We allow a number summed with addition, or a number.
This does in fact encompass infinite sequences of additions. This is
thanks to having the non-terminal addition on the right side of the sequence. addition can expand to another
addition, so this grammar can produce ASTs that look like this:
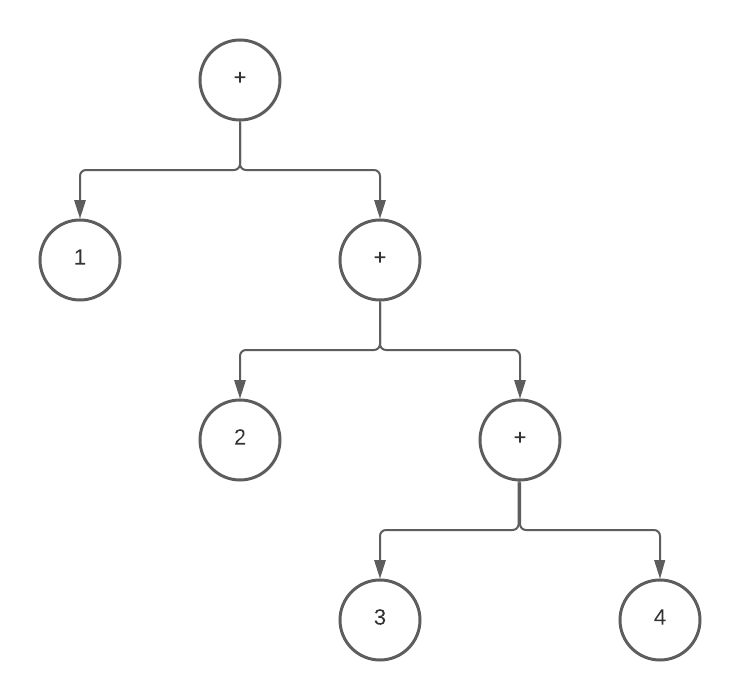
Right recursive AST
Modifying our code to account for our right recursive grammar changes this:
function addition (tokens) {
const additionLeft = addition(tokens);
...
into this:
function addition (tokens) {
const operandLeft = numberLiteral(tokens);
...
If we think through how this works, the only possible way we can have a valid addition, is to have a valid
number literal appear first. Number literals are terminal symbols, meaning in either case of having a valid number
literal, or an
invalid number literal, we will know if we have a valid addition before we attempt to derive another addition. I.e.
there won't be a recursive call to addition from addition, if there isn't a valid expression on the left side of
an expression first.
The rule of thumb I have been following throughout creation of my parser, is that as long as it's impossible for the left side of an expression to recursively reach itself before either failing, or consuming some tokens via a leaf expression, then the non-terminal expression is probably right recursive and fine.
Operator precedence
The next challenge is ensuring our grammar is unambiguous.
Our example covered addition expressions, but in any reasonable language we would cover the majority of mathematical expressions, such as subtraction, division, multiplication...
A first attempt at extending our grammar to include multiplication and subtraction might look like this:
<mathsExpression> ::= <addition> | <subtraction> | <multiplication>
<addition> ::= <numberLiteral> "+" <mathsExpression>
| <numberLiteral>
<subtraction> ::= <numberLiteral> "-" <mathsExpression>
| <numberLiteral>
<multiplication> ::= <numberLiteral> "*" <mathsExpression>
| <numberLiteral>
<numberLiteral> ::= LEAF
We've defined a new non-terminal which is simply a choice between all our mathematical operators: <mathsExpression>.
This can be any of our operators, eventually reaching our terminal symbol <numberExpression>.
This grammar will handle expressions like this just fine:
3 - 4 * 5 + 3
The problem is that in the real world, we typically give operators precedence. This defines the order in which operators which follow each other should be evaluated.
You might remember using the mnemonic BIDMAS at school like I did. This tells you the order operators should be evaluated. Brackets, then indices, then division, multiplication, addition, and finally subtraction. Whilst our above grammar will handle the three operators we have chosen to implement, it will not enforce any kind of order.
In fact it will create the following AST for our expression 3 - 4 * 5 + 3:
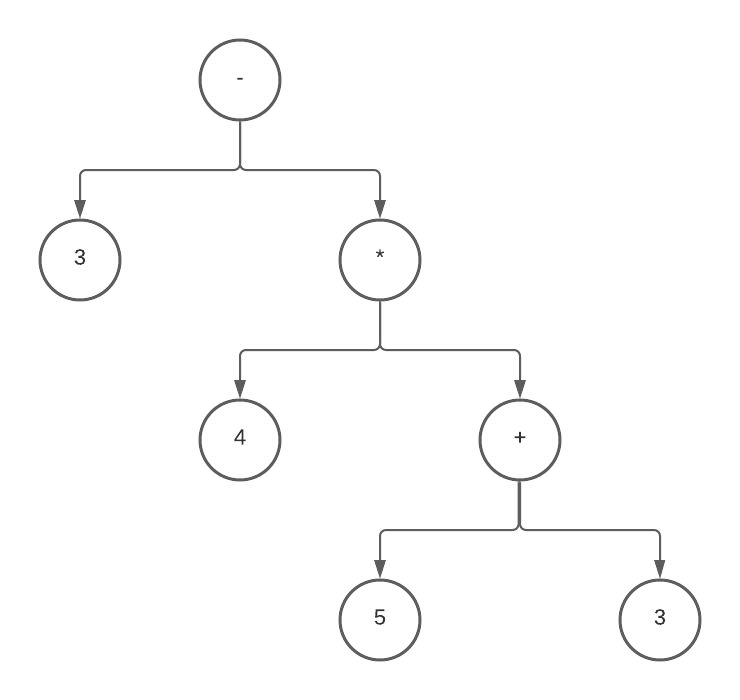
This is not correct if we want to respect the standard order of mathematical operators. The structure of the tree will determine the order that the operators get applied in, with subtraction being applied last. The AST is equivalent to:
3 - (4 * (5 + 3))
Thankfully it is possible to define a grammar that encapsulates operator precedence. To achieve this, we need to define separate non-terminal symbols which refer to each other, rather than saying "any of these mathematical operators is valid".
For example, we can define this grammar which will respect BIDMAS for our chosen operators:
<mathsExpression> ::= <subtractionExpression>
<subtractionExpression> ::= <additionExpression> "-" <mathsExpression>
| <additionExpression>
<additionExpression> ::= <multiplicationExpression> "+" <mathsExpression>
| <multiplicationExpression>
<multiplicationExpression> ::= <numberLiteral> "*" <mathsExpression>
| <numberLiteral>
<numberLiteral> ::= LEAF
This grammar forces operators with higher priority to appear lower down the tree. multiplicationExpression is
closest to our leaf, followed by addition, followed by subtraction, i.e. BIDMAS.
The only location that subtractionExpression can be matched in an expression with other operators
next to it, is
at the top of the tree. Any other operators that are either side of subtraction can only appear below subtraction in
the tree, i.e. they have higher priority. The same goes for addition, followed by multiplication.
Extending this idea to all operators which could be located in an expression, e.g. variables, results of function calls, whatever, we can define a long chain of operators ensuring there is no possible ambiguity in the expression.
The rule of thumb I have been following for operators that work over 2 operands like our standard math/boolean operators, is:
// top level expression
<expression> ::= <rule>
<rule> ::= <higherPriorityExpression> OPERATOR <expression>
| <higherPriorityExpression>
As you can imagine, this does start getting a bit unwieldy when you have a large number of operators. My parser currently has 17 operators chained together in this way. Tools like yacc allow you to specify grammars in the more natural way of matching any operator, along with a precedence rule, e.g. "going right means higher operator precedence" which is far nicer for comprehension of the grammar.
The code doesn't change much again from our previous attempt, we simply need to replace the left operand function call, with a call to the next step down in our operator chain.
function subtraction(tokens) {
const leftOperand = addition(tokens);
// The same as before, check the operator,
// then check for a valid expression on the RHS
...
function addition(tokens) {
const leftOperand = multiplication(tokens);
...
function multiplication(tokens) {
const leftOperand = division(tokens);
// And so on
...
Operator associativity
One last problem we will face with operators is operator associativity.
The problem arises because we are forced to use a right recursive grammar to remain compatible with recursive descent parsing. This tends to generate trees that are right-heavy, expressions will expand downwards and to the right. Humans on the other hand tend to read from left to right in Western nations.
If we have an expression:
3 - 4 - 5
Generally we will evaluate this in our head from left to right, so we will evaluate 3 - 4, then subtract 5 from
the result of this, giving us an answer of -6. But with a right recursive grammar, it will generate a tree that
will give us the opposite result, i.e. it will evaluate 4 - 5 first, then subtract this result from 3, giving us
the incorrect result of 4.
Chained identical operators do not have precedence over each other, and it is not possible to specify any kind of precedence within the grammar itself when using right recursion. A left recursive grammar would handle this correctly by default, but we need to take extra measures with right recursion.
Rewriting the AST for left associativity
The solution I have gone with in my parser is a post-processing step of an AST. It rewrites portions of the tree where two identical operators are spotted next to each other.
E.g. if it were to come across this AST:
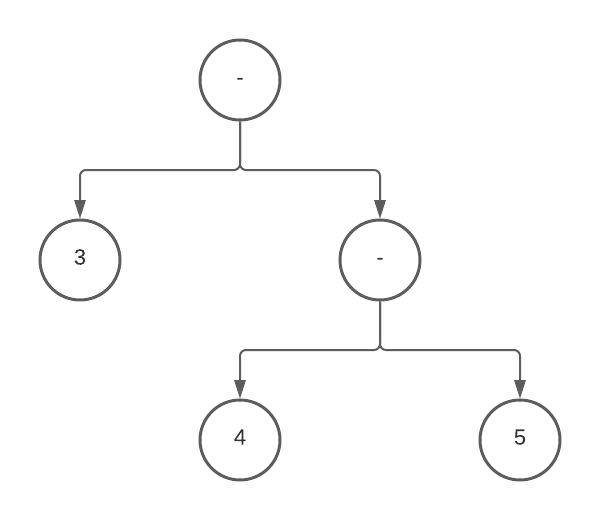
It would spot that there are two subtraction operators next to each other, lift the right hand side up, and push the left hand side down, producing this left associative AST instead:
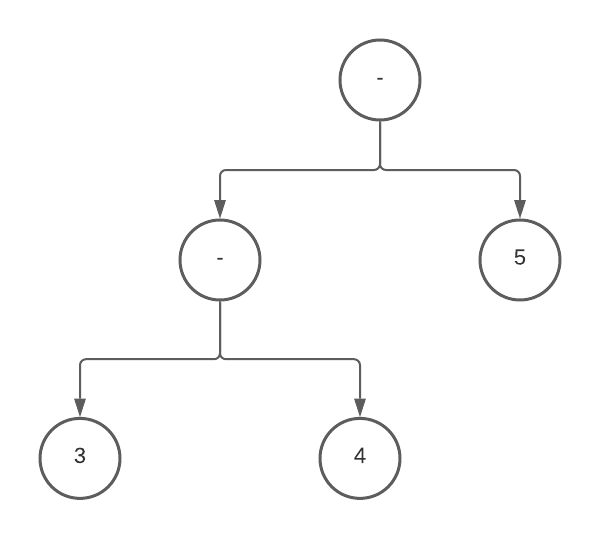
The code to do this is relatively straightforward, and is just juggling some nodes around in the tree:
// Function to convert all operator nodes in
// an AST to left-associative nodes
const operator = (ast) => {
if (ast.value.rightOperand?.type === ast.type) {
// `leftAssociate` is a function which is
// essentially a long switch statement on all
// possible types of node in our grammar, which
// calls functions associated with each specific
// node for handling their cases of left
// associativity
return leftAssociate(
// Lift up the right side to replace the current node
mergeDeep(ast.value.rightOperand, {
value: {
// Push the current node down into the left operand
leftOperand: mergeDeep(ast, {
value: {
// Replace the current node's right operand, with the
// left side of the right operand - referring to the
// images might make this a bit clearer
rightOperand: ast.value.rightOperand.value.leftOperand,
},
}),
},
}),
);
}
// Different operators, skip over this node and continue
// going down our AST to check the other nodes
return mergeDeep(ast, {
value: {
leftOperand: leftAssociate(ast.value.leftOperand),
rightOperand: leftAssociate(ast.value.rightOperand),
}
});
};
Summary
We got through quite a lot! We've looked at why I personally would want to create a programming language, hopefully giving you some ideas as to what you could do with your own toy programming language.
We looked at the main high level concepts required for creating a programming language - lexing, parsing and interpretation/compilation.
We went through in more detail how to actually create a lexer, a recursive descent parser, and how to handle most of the common problems you will see that are associated with right-recursive context free grammars.
In future posts I will go through in detail how I created my interpreter, as well as an implementation approach for handling functions and their closures.
Eventually I will also post about my goals, and if I managed to achieve them or not.